公務員試験の経済学で用いる数学は、基本的には中学時代までに習うことばかりです。ただし、高校時代に習うことも若干使います。その1つが微分です。
いま、「高校時代に習う」と書きました。しかし、微分は数学Ⅱの範囲です。数学Ⅰしか必履修でないことを考えますと、高校時代に進んだ科やコースによっては習わなかったという人もいらっしゃることでしょう。
そこで、本記事では、微分の計算方法についてかみ砕いて解説します。
1 そもそも微分とは?
微分が意味するところを、公務員試験の経済学で必要な形で理解しましょう。ずばり、ある関数のある点における傾きが微分によって求まるとおさえてください。
言い換えると、何かの関数を微分すると、それがその関数の任意の点に接する線(接線)の傾きを表しているということです。
数値例を出しましょう。\( y=x^2\)という関数があるとします。これを微分するとy’=2xです(この計算方法は後で説明します)。例えば、x=0.5を代入すると、y’=1となりますね。\(y=x^2\)のx=0.5付近に接線を引いた場合の傾きの大きさは1ということを示します。
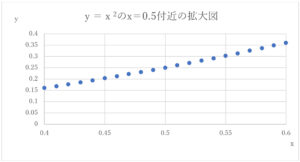
実際、下図(\(y=x^2\)を0.5付近で拡大したものです)を確認すると、横軸が0.05増えると、縦軸も0.05増えています。そもそも傾きは、「縦軸の変化分÷横軸の変化分」で出しますが、これで出すと0.05÷0.05=1となり、先ほどのy’=1と一致します。
もう一つ見てみましょう。x=0.6付近にします。y’=2xにx=0.6を代入してy’=1.2を得ます。下図で0.55から0.6へ横軸が増えたときの縦軸の変化分を確認すると、0.05よりも大きそうです。なぜなら、0.35より大きいy値がプロットされているからです。0.36くらいといえそうです。これで、0.06÷0.05=1.2となり、これまたy’=1.2と一致します。
以上から、y’=2xは\(y=x^2\)のある点における傾きを求める式が得られると分かりました。このように、微分をすると、ある関数のある点における傾きが求められるようになります。
2 なぜ経済学で微分を用いるのか
これまでの説明で、微分が何を意味するかは分かって頂けたと思います。次に、読者の皆様が思うのは、これがどうして経済学に必要なのかということでしょう。
そこで、この点について、「企業の利潤最大化を求めるときに使う」という例を取り上げて示しておきます。もちろん、経済学の他の分野でも使うのですが、あくまで使うときの一例です。
そもそも、公務員試験の経済学では、企業の行動原理について、利潤最大化を追い求めると仮定します。そして、利潤式は、π(利潤)=TR(総収入)-TC(総費用)だと考えます。
このとき、頻出問題において、総収入や総費用は、生産量\(x\)を用いて表した式で与えられます。
まぁ、総収入は販売している価格Pに販売量x(=全て売れていると考え、生産量と同じになる)を掛け合わせるPxで表現されるのは、そこまで違和感のない仮定でしょうね。また、総費用も、生産量に伴って仕入れる原材料や人件費がかかりそうだから、無茶な設定ではないといえます。
ここでは、価格を100円として、生産量はxのままとします。総収入は、TR=100xです。総費用は\(TC=2x^2\)としましょう。利潤式は、\(π=100x-2x^2\)です。xの値でただ1つの利潤πが求まるので、利潤式=利潤関数といえるので、以下から利潤関数と書きますね。
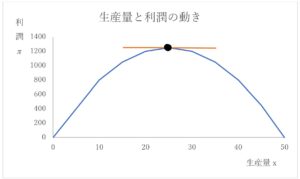
さて、利潤関数を描くと、以下のような形となります。
では、利潤最大化のときの生産量はどのように出せばいいでしょうか。グラフからは、生産量の20~30の間と分かると思いますから、利潤関数のxに考え得る生産量を21、22、23と代入しながら最大の値を出しましょうか。
それは時間がかかりすぎます。そもそも、このグラフを書く作業も加味して考えれば、しんどすぎます。とても試験本番にやっていられません。
ここで、微分が活躍します。微分はある関数のある点における傾きを出すんでしたよね。そして、上図で利潤関数の最大値の点を通る接線を描いてみると分かるのですが、最大値の点においては傾きの大きさが0(ゼロ)となっています(図の中黒点では、接線(オレンジ線)が横軸に平行にひかれています)。
つまり、π’(利潤関数を微分する)=0です。\(π=100x-2x^2\)を微分すると、π’=-4x+100なのですが(計算手順は後述します)、これが0(ゼロ)となります。すなわち、
-4x+100=0
が成立します。この方程式をとけば、x=25が出てきます。この生産量のとき、利潤は最大値となります。
一応、懸案の20<x<30の中の値を確認しますと以下です。
x=25のときが利潤最大だと分かります。上で出した計算結果と一致しますね。
このように、微分して出てきた式が0(ゼロ)だという方程式をつくると、ある関数の最大値や最小値が分かります。したがって、利潤最大化問題のような出題分野では微分が大いに用いられます。
経済学で微分を使うイメージができましたでしょうか。次の項目でいよいよ、微分の計算方法を解説します。
3 微分の計算方法
それでは、微分の計算方法を示しましょう。ただし、どうしてこのような計算方法になるのかという証明は割愛します。なぜなら、その点は公務員試験に出ないからです。皆さんには、\(y=x^2\)を微分するとy’=2xとなるような処理方法の法則を覚えていただきます。
以下の例題①~⑤を使います。

いずれにもある\(\frac{△U}{△y}\)は、関数Uを、yで微分するという意味です。つまり、U’の意味するところと同じです。「△」はデルタと読みます。「δ」や「d」で書かれる参考書や本もあります。いずれも変化量という意味です(本記事は「Δ」と記載します)。
では、①をみてください。指数の3が前に出て(3×y3)、その後に指数は3から1つ減って2になっています(3×y2で3y2)。このように、指数を前に出して、1つ指数が減るという処理をしてください。
②もその処理は同じです。①と違うのは、係数と掛け算をしているということですね。具体的には、「3y2」は指数の2が前に出て「2×3=6y2」と係数との掛け算をして、その後に指数は2から1つ減って「6y」です(y1はyと書きますよね)。ちなみに、y0=1ですから、U=yをyについて微分する場合は、\(\frac{△U}{△y}=1\)となります。
③の「27」が微分すると「0」ということですが、これはすなわち、定数を微分すると「0」になるということを意味します。
④⑤は微分する文字でないものは定数と同じに扱うということです。ちなみに、こういう微分を偏微分といいます。
④の具体的な計算過程は以下です。上がxで微分し、下がyで微分しています。
\(\frac{△U}{△x}\)=0.5・6x0.5-1=3\(\frac{1}{x^{0.5}}\)=\(\frac{3}{x^{0.5}}\)=\(\frac{3}{\sqrt{x}}\)=\(\frac{3\sqrt{x}}{x}\)
注)最後のところは、分母を有理化しています。
\(\frac{△U}{△y}\)=1・2y1-1=2y0=2×1=2
⑤の具体的な計算過程は以下です。上がxで微分し、下がyで微分しています。
\(\frac{△U}{△x}\)==2・3x2-1y3=6xy3
\(\frac{△U}{△y}\)=3・3x2y3-1=9x2y2
以上の例を通じ、具体的な処理方法を覚えていただければ大丈夫です。
まとめ
経済学では、取り上げた利潤最大化問題だけでなく、効用最大化問題、〇〇弾力性(例;需要の価格弾力性)など、色々な単元の出題問題を解くために、微分の計算ができなければなりません。
本記事内容で法則を理解したら、微分の計算練習をたくさんしておきましょう。分かることとできることはしばしば乖離します。練習を積み重ねて、微分の計算がスイスイできるように是非なってください。応援しています。
なお、究進塾では、経済学の個別指導講座があります。数的処理を含め、ブログ以上にしっかりと経済学を理解したい、過去問が解けないから教えて欲しいなどの疑問にとことん付き合います。よろしければ、ご受講ご検討ください(詳細は、経済学対策講座をご覧ください)。


 個別指導講座
個別指導講座 お問い合わせ
お問い合わせ