【問題】
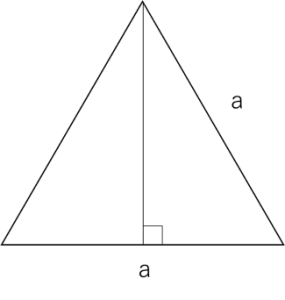
次の図のように、側辺が底面に垂直に見える方向から見ると、一辺の長さが aの正三角形に見える正四角錐がある。この正四角錐の表面積はどれか。(特別区2002)
1:(1+√7)a2
2:\(\frac{(1+√7)}{2} \)a2
3:\(\frac{(2+√7)}{3} \)a2
4:\(\frac{(3+√7)}{4} \)a2
5:\(\frac{(4+√7)}{5} \)a2
立体の表面積の問題です。中でも勘違いしやすい錐の問題です。
立体について解説します。
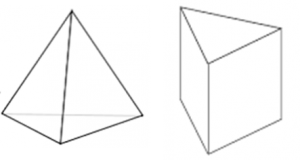
錐という立体は先端が尖っている形を表します。柱という立体は先端が尖っていない形を表します。
左:三角錐
右:三角柱
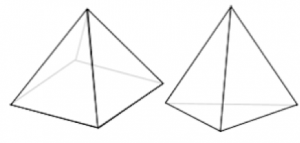
正三角錐と正四角錐もよく間違いやすいのですが、底面の形が三角形か四角型かによって判断できます。図に書くと下記の通りです。
左:四角錐
右:三角錐
次に表面積について解説します。
表面積を問う問題では 、その立体の展開図を書くことが第一歩です。四角錐の展開図は下記のようになります。三角形が4つ、四角形が1つから構成されていることがわかります。
つまり三角形の面積を求めてそれを4倍し、四角形の面積を求めて、それらを合計すれば答えが求められます。
問題を見てみましょう。
側辺という聞きなれない言葉があります。これは四角錐の底面から頂点に向かって伸びる辺のことです。この立体を横から見たことを考えて、一つの側辺がちょうど三角形の底面に垂直に刺さっているように見えた場合を考えます。この時底辺の長さは a のように見えたようです。
ということは、実際の底面の形はどのようになっているのでしょうか?
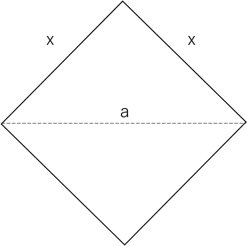
この見方だと、底面の一辺ではなく、底面の対角線の長さが a であることがわかります。
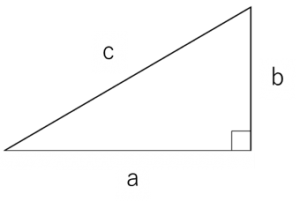
よってまずは底面の一辺の長さを求めることを考えたいと思います。図形の長さを求めたい時は、求めたい長さが含まれる図形に着目することです。そうすると求めたい辺の長さを x とすると、辺の長さが で構成される直角二等辺三角形が見つかります。
直角三角形の辺の長さを求めるには、三平方の定理が有効です。公式は次のようでした。
これに当てはめて考えるとき、式は次のようになります。
x2 + x2 = a2
計算すると、
2x2 = a2
⇔ x2 = \(\frac{1}{2} \)a 2
⇔ x = \(\frac{1}{√2} \)a
一辺の長さが求まりました。ここで四角錐の底面の部分の面積が求められます。
x×x = x2 = \(\frac{1}{2} \)a 2
次に四角錐の三角形の部分の面積について考えていきましょう。
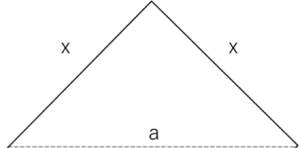
求めたい辺の長さを x とします。三角形の部分に着目すると辺の長さが分かっているのは図のようになります。
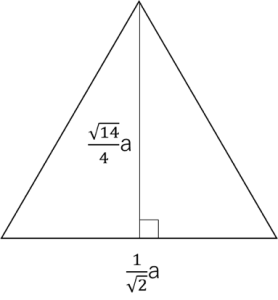
底辺に垂直な辺の長さがまだ分かっていません。この辺の長さが欲しいのでこの辺を含む図形がないか考えていきます。そうすると、図のような二等辺三角形があることがわかります。これも直角三角形なので、三平方の定理が使えます。
辺の長さを求めると次のようになります。
x2 + (\(\frac{1}{2√2} \)a)2 = a2
⇔ x2 = \(\frac{7}{8} \)a2
x = \(\frac{√14}{4} \)a
三角形の高さを求めることができました。
よって、三角形1つ分の面積は次のようになります。
\(\frac{1}{√2} \)a × \(\frac{√14}{4} \)a ÷2 = \(\frac{√7}{8} \)a2
したがって、立体の表面積は次のようになります。
(立体の表面積)=(三角形の面積)×4+(底面の正方形の面積)
= \(\frac{√7}{8} \)a2 × 4 + \(\frac{1}{2} \)a2
= \(\frac{(1+√7)}{2} \)a2
よって答えは2番とわかります。


 個別指導講座
個別指導講座 お問い合わせ
お問い合わせ