150人の生徒がいる。サッカーと野球が好きか調査したところ、サッカーが好きな生徒の8割は野球が好きであり、野球が好きな生徒の6割はサッカーが好きであることがわかった。どちらも好きではない生徒が35人であるとき、サッカーが好きな生徒は何人いるか。市役所(2012)

1：60人
2：68人
3：75人
4：84人
5：90人

集合算の問題です。集合算のコツは、ベン図を描いてその中の変数を用いた式を立てて、 文字消去しながら計算を進めていくことです。

ベン図の描き方については、問題文を例にとって考えていきましょう。

問題文を見てみると、サッカーが好きな人と野球が好きな人がいることがわかります。そして両方とも好きな生徒も、両方とも好きではない生徒もいます。図に書くと次のようになります。

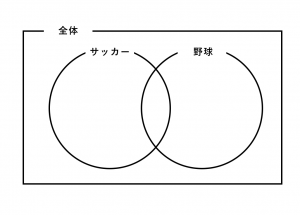
この中に、考えやすいように次のように変数を置きます。

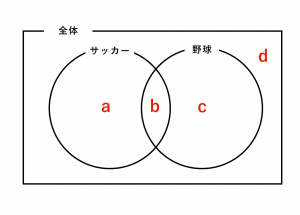
変数を置いたら問題文を見ていきましょう。

「150人の生徒がいる。」

全体にはa、b、c、dがあるので、a + b + c + d = 150…① とわかります。

「サッカーが好きな生徒の8割は野球が好きであり、」

サッカーが好きな人はa+bです。両方が好きな人はbになります。

サッカーが好きな人の8割は両方好きなので、式を立てると、

0.8(a+b) = b…②

「野球が好きな生徒の6割はサッカーが好きであることがわかった。」

野球が好きな人はb+cです。両方が好きな人は同じくbになります。

野球が好きな人の6割は両方好きなので、式を立てると、

0.6(b+c) = b…③

「どちらも好きではない生徒が35人であるとき」

これはシンプルですね。d = 35…④とわかります。

①～④について解くと、④を①に代入して、

a + b + c = 115…①’

②③を式変形すると、

8a = 2b ⇔ 4a = b…②’
6c = 4b ⇔ 3c = 2b…③’

②’③’を①‘に代入しやすくすることを考えます。

②’③’を見ると、どちらもbの式で書かれています。aとcを消せば、①’の式はbだけの式になるので、bが求められるとわかります。

よって、「a＝〇〇」、 「c＝△△」のように式変形しましょう。

a = \(\frac{b}{4}\)…②’’

c = \(\frac{2b}{3}\)…③’’

②’’③’’を①’に代入すると、

\(\frac{b}{4}\) + b + \(\frac{2b}{3}\) = 115

両辺を12倍すると、

3b +12b +8b = 1380
⇔23b = 1380
⇔b = 60

②’より、4a = 60 ⇔a = 15

問題文よりサッカーが好きな生徒の数を問われているので、

a + b = 15 + 60 = 75

よって正解は3番だとわかります。