ある工場で2種類の製品A、Bが製造されており製品一個当たりの人件費原料費ならびに製品を出荷する際の製品単価がそれぞれ表のとおりであるとする人件費の上限は130万円、原料費の上限220万円である時製品A、Bの出荷額の合計の最大値はいくらか。国家Ⅰ種(2009)
(単位:万円)
| 人件費 | 原料費 | 製品単価 | |
| 製品A | 3 | 4 | 12 |
| 製品B | 2 | 5 | 10 |
1:560万円
2:580万円
3:600万円
4:620万円
5:640万円
ある条件の中で最大最小を問われる問題です。
この問題文を見てすぐに分からなくてもいいのですが、方程式を作り、 グラフを書いて考えます。連立方程式の解として考えてもいいです。これらは後述しますので、問題文を読み解きながら考えていきましょう。
問題文を見ると、人件費の上限が最大130万円までと決められています。
例えば製品 A を10個製品 B を10個作った場合、30 + 20 = 50万円となり、条件はまだまだ超えなさそうです。
製品 A を20個製品 B を30個作った場合、60+60 = 120万円となり、もうすぐ超えてしまいそうです。
このような形で製品 A と B を何個ずつ作ると上限を超えないか?を考えます。製品 A B とも何個ずつかわからないので製品 A を x 個、製品 B を y 個とおきます。そうすると次のような式が立てられます。
3x + 2y < 130…①
原料費の方も同様に式を立ててみましょう。
4x + 5y < 220…②
二つの式を「y=」に式変形してグラフに書くと次のようになります。
y < -\(\frac{3}{2}\)x + 65…①’
y < -\(\frac{4}{5}\)x + 44…②’
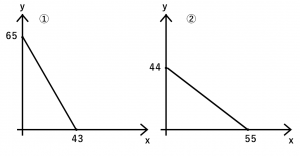
これらの両条件を満たす斜線部分(下図)が、問題文の人件費の上限と原料費の上限に合うところです。車線部分のいずれかの部分が最大となります。
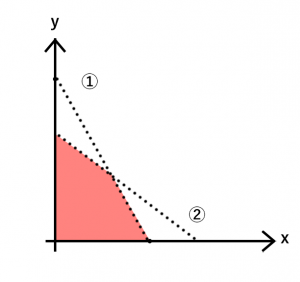
一見両者の直線の交点である尖った部分が最大になりそうです。しかし次の図のような場合だと、二つのグラフのx切片とy切片が答えになってしまいます。
x切片が答えなのかy切片が答えなのか、それとも両者のグラフの交点が答えなのか、それらを判断するために、製品単価の直線も考えてみましょう。
一見両者の直線の交点である尖った部分が最大になりそうです。
製品単価も同様にAがx個、Bがy個の時を考えます。
ここで、製品単価を製品の個数とかけてみると次のようになります。
12x + 10y
この値は求めるべき製品 A、Bの出荷額の合計の最大値となるので、何か文字でおいてあげましょう。条件の最大最小問題の時にはkと置くことが多いです。よって次のようになります。
12x + 10y = k…③
この式③を「y=」のかたちに変形すると次のようになります。
y = -\(\frac{6}{5}\)x + \(\frac{k}{10}\)…③’
この時の直線の傾きを①’②と比較して見てみると、
\(\frac{4}{5}\) < \(\frac{6}{5}\) < \(\frac{3}{2}\) = 0.8 < 1.2 < 1.5
より、③’は①’②’の両者の式の傾きのちょうど間であることがわかります。
傾きがこの二つよりも大きいと x 切片が答えに、傾きがこの二つよりも小さいとy切片が答えになります。下の図を見ていただけるとイメージが湧くかと思います。
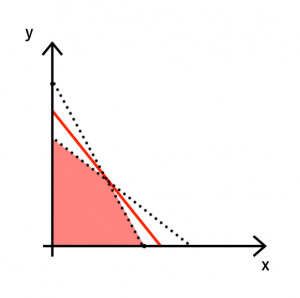
よって①②のグラフの交点座標が最大の出荷額となるときの個数になるので、これを求めます。
-\(\frac{3}{2}\)x + 65 = -\(\frac{4}{5}\)x
x = 30
y = -\(\frac{3}{2}\)×30 + 65 = -45 + 65 = 20
x, yを求めることができました。
③に代入すると、
k = 12×30 + 10×20 = 560
よって答えは1番だと分かりました。


 個別指導講座
個別指導講座 お問い合わせ
お問い合わせ



