個別指導講座
お問い合わせ
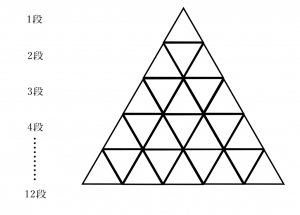
次の図のように同じ長さの辺で作った小さな正三角形を組み合わせて大きな正三角形を作っていくとき、12段組み合わせるのに必要な線の合計の本数はどれか。地方上級(2009)
1： 198本
2： 216本
3： 228本
4： 234本
5： 252本
等差数列の問題です。等差数列とは一定の数を足しながら増えていく数列のことで次のように表されます。
a1, a2, a3, …, an
左から順に1項目、2項目と言い、aの右の小さな添え字を項数と言います。a1からa2に進むためには公差と呼ばれる値を足すことで次の項に進めます。公差にはdがよく使われます。よって次の式が成り立ちます。
a1 + d = a2, a2 + d = a3, …, an-1 + d = an
公式として、a1を初項、公差をｄ、項数をnとすると、次のような式が成り立ちます。
an = a1 + d×(n – 1)
anのようにn項目までを文字にして表すことを一般化とも言います。
そしてその和の公式は次のようになっています。a1からanまでの和をSnとすると、
Sn =\(\frac{n×(a_1 + a_n)}{2}\)
a1, a2, a3, …, an
左から順に1項目、2項目と言い、aの右の小さな添え字を項数と言います。a1からa2に進むためには公差と呼ばれる値を足すことで次の項に進めます。公差にはdがよく使われます。よって次の式が成り立ちます。
a1 + d = a2, a2 + d = a3, …, an-1 + d = an
公式として、a1を初項、公差をｄ、項数をnとすると、次のような式が成り立ちます。
an = a1 + d×(n – 1)
anのようにn項目までを文字にして表すことを一般化とも言います。
そしてその和の公式は次のようになっています。a1からanまでの和をSnとすると、
Sn =\(\frac{n×(a_1 + a_n)}{2}\)
問題文を見てみましょう。
1段目と2段目と3段目と4段目の絵が書いてあるのでそれぞれ線の本数を数えてみましょう。
そうすると次のように数えられました。
1段目: 3本、2段目: 6本、3段目: 9本、4段目: 12本
それぞれの数字の関係性を見てみると3から始まって3ずつ増えていることがわかります。
よって等差数列の公式に当てはめて考えると、次のように書けます。
初項が3、公差が3なので、
an = a1 + (n – 1)×d = 3 + (n – 1)×3 = 3n
問題文では12段目のところまで考える必要があります。
12段目までなので項数nは12として考えると、等差数列の和の公式に当てはめて次のようになります。
S12 = \(\frac{12×(3 + 3×12)}{2}\) = 234
よって答えは4番となります。
