次のア～エは、それぞれ一定の規則により並んだ数列であるが、空欄 A～D に当てはまる4つの数の和として正しいのはどれか。地方上級(2012)

ア　1, 5, 13, A, 61, …
イ　2, 8, 44, 260, B, …
ウ　3, 11, 43, C, 683, …
エ　4, 14, 42, 88, D, …

1:1908
2:1918
3:1928
4:1938
5:1948

階差数列の問題です。階差数列とは、数列a_nの隣り合う二つの項の差を項とする数列ｂ_ｎのことです。

一般的に次のような式で表されます。

b_n = a_n+1 – a_n

こう書くと難しいですが、図で考えると分かりやすいでしょう。

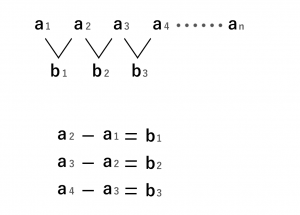
この図に当てはめて、アから考えてみます。

1,5,13の間には規則性がすぐには見つかりません。それぞれの差を取ってみましょう。そして先ほどの図に当てはめて考えてみましょう。

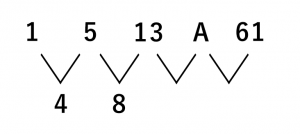
そうすると間の数値が4、8であることがわかりました。初項は1ですが、これに4を足すと次の5になり、この5に8を足すと13になることがわかります。

次の A の値が分からず、さらにその次は61になっています。4、8の次にどのような値をとればAになり、さらにその次の値を足せば61になるかを考えます。

4, 8という数字の並びを見ると4ずつ出されているか、2倍にされているか、どちらかが考えられます。

4ずつ足されている場合は4, 8, 12, 16という数の並びになります。2倍ずつされている場合は4, 8, 16, 32という数の並びになります。

4ずつ出された方を考えてみるとAは25になります。25に16を足すと41になるので61と合いません。

2倍ずつ増えた方を考えてみると、13に16を足すと A は29になります29に32を足すと61になります。こちらの方であっていることが分かるので A は29であるとわかります。

同じ要領でイの問題も考えていきましょう。

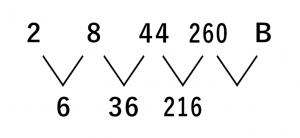
こちらも同様に2, 8, 44, 260の間に規則性は見えないので両者の差を取ってみます。すると両者の差は6, 36, 216とわかります。

6, 36, 216という並びから数字の桁の増え方が大きいので掛け算かなと予測できればより良いでしょう。6に何をかけたら36になるかというと6だとわかります。

36から216のところはイメージしづらいかもしれませんが、この規則性を用いて6をかけると216になることがわかります。よって、次のBの値を求めるには、260に216×6をしたものを足せば良いとわかります。

計算すると、260 + 216×6 = 216 + 1296 = 1556

よって B の値は1556とわかりました。

次にウの問題も解いていきましょう。

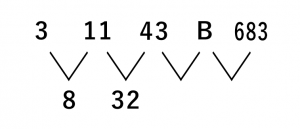
こちらも同様に3, 11, 43からは規則性は見いだせません。これらの数字の間の数字を考えると8, 32と分かります。

アの問題の時と同じように、これは24ずつ増えているのか、4倍ずつされているのかどちらかであると考えられます。

24ずつ増えているのであれば、8,32,56,80と増えていることがわかります。

4倍ずつ増えているのであれば、8,32,128,512と増えていることがわかります。

24ずつ増えていると考えるとすると、43に56を足して99、99に80を足して179となります。これは683とは合いません。

4倍ずつ増えているとすると43に128を出して171、171に12を足して683となり問題文に合うことがわかります。よって C は171であることがわかります。

最後にエの問題も見てみましょう。これは少し難しいです。

4, 14, 42, 88ではまた規則性が見出せません。同様にしてこれらの差を取ってみましょう。

すると10, 28, 46 となるのですが、これもまた規則性が見出せません。さらにこれが階差数列になっていることを考えて、 それぞれの項の差を取ってみましょう。

そうすると18, 18となり、18ずつ増えていっていることがわかります。二重の階差数列になっていたようです。

数式で考えるとややこしいのですが、次のように図で考えると分かりやすいでしょう。

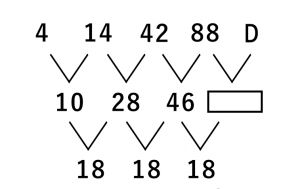
元の数列の88の次の項を考えるには、88に階差数列の4項目を足す必要があります。これを求めるには46に18を足せばいいと分かるのでそれが64であることがわかります。図の□が64になります。

88に64を足すと152となります。よって D が求められました。

元の問題に立ち返ると A から D の和がいくつか？であるので、それぞれ足し算すると、

A + B + C + D = 29 + 1556 + 171 + 152 = 1908

よって答えは1番が正しいとわかります。