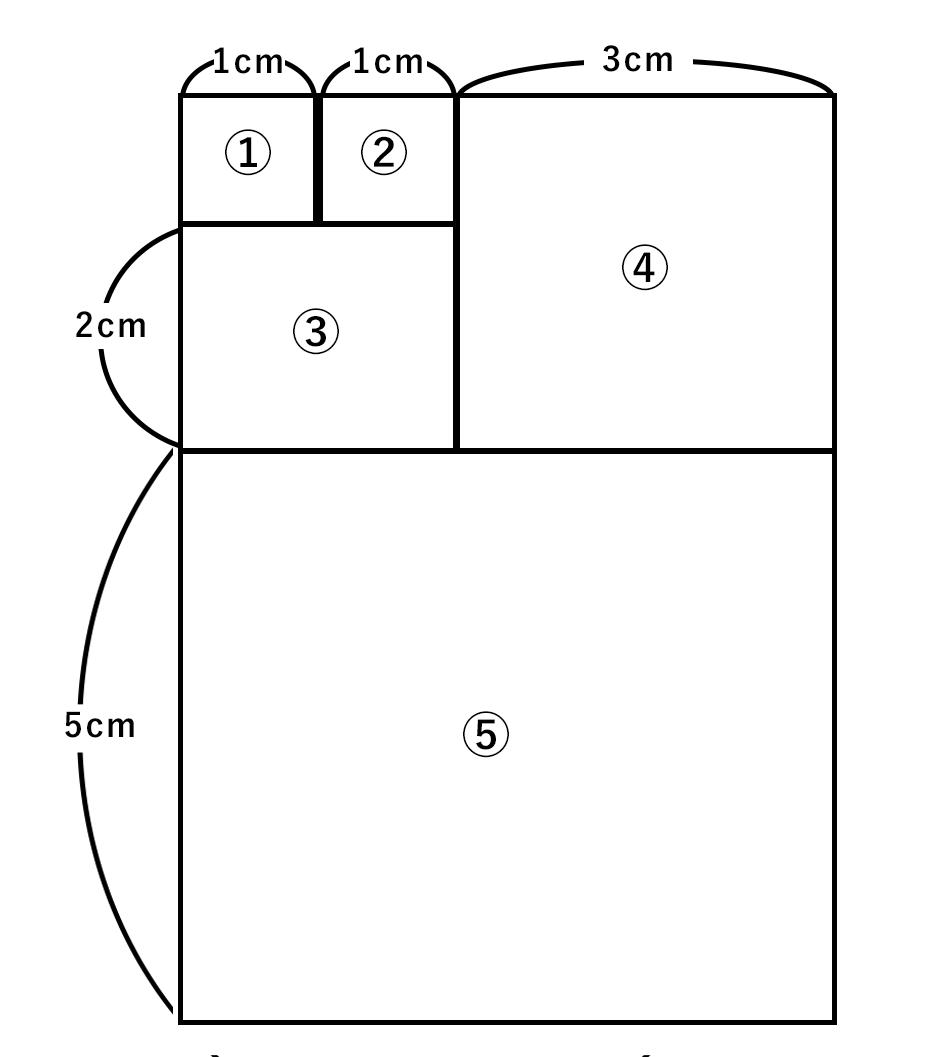
図の①②の四角形は、1辺の長さが1 cm の正方形である。この2枚を並べてできた長方形に③④⑤というように、長方形の長辺と1辺の長さが等しい正方形を加えることを繰り返していく。何回目かに加える正方形の一辺は610 cm になるが、この610 cm の正方形を加える1回前に加えた正方形の1辺の長さとして正しいのはどれか。市役所(2015)

1：233㎝
2：288㎝
3：322㎝
4：377㎝
5：411㎝

フィボナッチ数列の問題です。フィボナッチ数列を知っている人だと、いきなり答えが4番だと分かる人もいると思います。

フィボナッチ数列とは
「1,1」から始まり、1, 1, 2, 3, 5, 8, 13, 21…
というように書かれます。

特徴としては、前の2つの数の和が次の方になっているということです。

例えば
1+1=2
1+2=3
2+3=5
⋮
といった形で増えていきます

あらかじめフィボナッチ数列を知っていると有利ですが、今回はこれがフィボナッチ数列と知らない体ていでそれに気づくまでを考えていきたいと思います。

問題を見てみると、①②の正方形を足して長辺が2 cm になるような長方形ができたところまで考えてみましょう。

この長辺2 cm に合うような正方形③をくっつけるので1辺が2 cm の正方形をくっつけます。この時に出来上がった長方形を見てみると1 + 2 = 3cmになっていることがわかります。

よって次にくっつける正方形の1辺の長さは3cmであることがわかります。そして2 + 3 = 5 cm が長辺となる長方形ができたことがわかります。長辺が5 cm なので次にくっつける正方形も5 cm だとわかります。

といった具合で、次の正方形の1辺の長さは、2つ前と1つ前の辺の長さから決まることが規則性として見て取られました。図で見てもそれが分かるかと思います。

この規則性から、数字を書き出していくと次のようになります。

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610

問題文にある610という数が出てきました。 よってこの規則性は考え方として正しいとわかります。

よって正解は4番だとわかります。