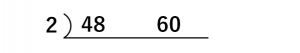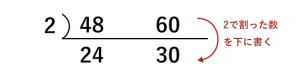【問題】
三つの自然数14,63, n は最大公約数が7で最小公倍数が882である。nが300より小さいとき自然数nは全部で何個か。特別区(2016）

最小公倍数の求め方と最大公約数の求め方について確認してみましょう。すでに分かっている場合は飛ばしてください。

まずは数字が２つの場合について見ていきますので、48と60の最小公倍数と最大公約数がいくつかを求めてみます。

まず、数字を列挙します。

その左隣に、これらの数字を割ることができる簡単な数字を書きます。

そして、この数字でそれぞれの数字を割り算していて、出た数字を下に書きます。

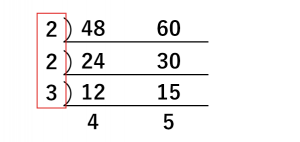
同様に繰り返し、割れなくなるまで繰り返すと次のようになります。

下図の赤枠を掛け算すると2×2×3 =12となり、これが48と60の最大公約数になります。

下図のL字の青枠を掛け算すると2×2×3×4×5 = 240となり、これが48と60の最小公倍数になります。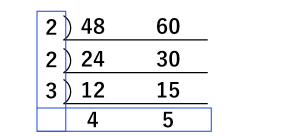

数字が３つ以上の場合は、先程と一部異なる点があるので、解説します。

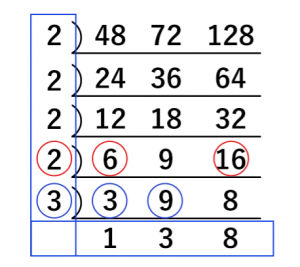
例として48, 72, 128の最小公倍数、最大公約数を考えましょう。

まずは同様に３つの数字を書き並べます。

３つの数字が共通して割ることのできる数字で割り算します。数字が２つのときと同様にこれ以上割れなくなるまで続けます。このときの赤枠が最大公約数です。2×2×2 = 8となります。これは数字が２つの時と同じです。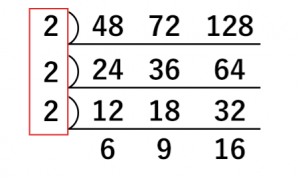

最小公倍数を求めるにはまだ続きがあります。

今度は３つ共通でなくても良いので、２つに共通する数字で割っていきます。図の赤丸部分では２で割れるので２で割ります。

このとき割り算しなかった９についてはそのまま下の段に降ろします。

青丸部分では３で割り算できるので、同様に３で割り、割れなかった８はそのまま下の段に降ろします。

そしてこの図の中の L 字型の枠内の数字を全てかけると48, 72, 128の最小公倍数になります。2×2×2×2×3×1×3×8 = 1152となります。

これらが最小公倍数と最大公約数の求め方です。それぞれ覚えておきましょう。

では問題を見ていきましょう。

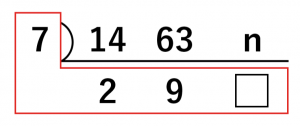
14, 63,  n をそれぞれ列挙していきます。

14と63はそれぞれ7で割り切れるので、縦列には7と書きましょう。nは7で割るといくらになるかわからないので、□と置きましょう。（もちろん文字で置いても良いです）

割り算すると以下のようになります。

問題文にもありましたが、最小公倍数は7とありました。すでに2と9に共通の約数はありませんが、縦列は7が1つあるだけで最小公倍数は7となるので問題ありません。

次に最大公約数について考えましょう。最大公約数はこの L 字型の所を全て掛け算します。掛け算した結果が882になるはずです。

式を立てると、次のようになります。

7×2×9×□=882

よって□ = 7となります。よって、□ = 7の場合は、n = 49となります。

次に、 n に入る他の数がないか考えます。

上記より 四角が7の時は n が49だと分かりました。しかし、最大公約数が882である条件を満たす n は他にもあるようです。問題文より、nは300より小さいという条件があるので、こちらを元に考えてみましょう。

n を満たす最小の数は49です。１倍2倍3倍としていくと、1倍：49、2倍：98、3倍：147、4倍：196、5倍：245、6倍：294、となります。７倍以上は300を超えてしまいます。

nの箇所にこれらの数字を当てはめてみると、1,2,3,6倍した時の49,98,147,294だと最小公倍数が882になります。

よって正解は３番だとわかります。