ある鉄道において、時速140 km の上りの特急列車は時速40 km の下りの普通列車と3分おきに出会った。この時、時速80km の上りの列車の準急列車が、下りの普通列車とすれ違い終わってから次の普通列車と出会うまでの時間として正しいのはどれか。
なお、上りの準急列車と下りの普通列車の長さはそれぞれ250mである。国税専門官(2001)
1: 4分
2: 4分15秒
3: 4分30秒
4: 4分45秒
5: 5分
通過算に関する問題です。
文章の中で、「すれ違った」、「追い越した」などが出てきたら通過算の問題かもしれないと思いましょう。
通過算に関しては、「すれ違うタイプ」と「追い越すタイプ」の2通りを公式のようにして覚えてしまってもいいかもしれません。
しかし、 どっちがどっちだか分からなくなってしまわないように、 今回はそれぞれの式の意味と、間違っている方はなぜ間違いなのかというところにも焦点を絞ってみたいと思います。
問題を見ていきましょう。文章問題なので図を書きながら考えていきます。
「時速140 km の上りの特急列車は時速40 km の下りの普通列車と3分おきに出会った。」
まずは速さについて考えていきましょう。 二つの列車はお互いに向かい合って走行しています。
時速140 kmで走っている電車に、自分が乗っているとイメージしてみてください。反対車線を時速40 km の列車がこちらに向かって走ってきました。このとき、自分が電車に乗っていない時よりも反対車線の電車の速度は40 km よりも速く見えるはずです。
これは自分が電車に乗っていない時に時速140km+時速40km = 時速180kmの列車とすれ違ったのと同じ速さになります。実際に車や電車に乗っていた時のことをイメージしてみると分かりやすいと思います。
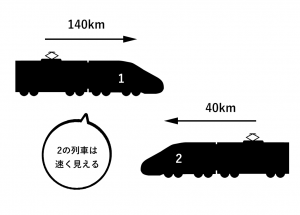
このとき、時速140km-時速40km=時速100kmとしてしまうのは本問では間違いです。これでは、実際に 自分の乗っている列車よりも遅い速さで移動してしまうことになります。
これは同じ方向で走行している時に、時速140kmの列車が時速40kmの列車を追い抜く速さと同じことになります。
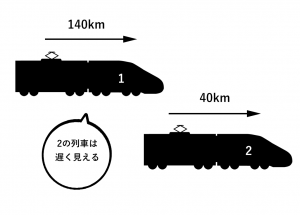
追い越す時はプラス追い抜く時はマイナス、と覚えてしまっても良いのですが、わからなくなった時には、実際に自分が車や電車に乗っていた時のことを思い出してどちらが正解なのか考えてみましょう。
出会った直後をスタートとして、 次に出会うまでをゴールとして考えます。それまでの間、時間は3分かかったという風に考え直すことができます。
まとめると、「時速180 km の 列車が3分間走り続けると、次の列車に出会う」ということと同じことになります。走った距離は書かれていないのでわかりません。
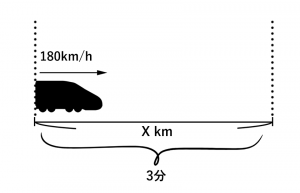
※時速、分速、秒速、km, m, cm の換算もできるようにしておきましょう。
1km = 1000m,1m = 100cm, 1時間 = 60分、1分 = 60秒で換算します。
時速40kmを40km/hと書いたりもしますが、40km ÷ 1時間と同じ意味です。これを分速〇kmで表すときは、40km ÷ 60分と同じです。落ち着いて計算しましょう。
距離をXと置くと、
X = 180 (km/時間) × 3 (分) ※距離=速さ×時間
= \(\frac{180 (km)}{1(時間)}\) ×\(\frac{3}{60}\)(分)
= 9 (km)
よって、列車同士が出会って、次の列車同士が出会うまでの間隔は9 km であることがわかりました。
次の文章に進みます。
「この時、時速80km の上りの列車の準急列車が、下りの普通列車とすれ違い終わってから 次の普通列車と出会うまでの時間として正しいのはどれか。なお、上りの準急列車と下りの普通列車の長さはそれぞれ250m である。」
下りの普通列車とありますが、速さに関する情報がないので、これは先程の時速40 km の普通列車と読み替えて解いてみましょう。
もう一方の列車の速度が、最初の文章と変わっています。時速80 km になっているので、先ほどと同様にして計算すると、時速180 km+ 時速40km = 時速120kmより、 時速120 km で走っている列車が普通列車と出会って、9 km 先の次の普通列車と出会うまでの時間を求められることがわかります。
図を書いてみると下記のような形になります。時間はTと置きました。
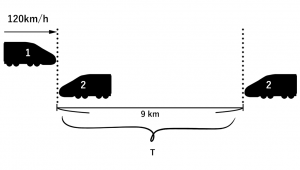
Tについて以下のとおり計算します。
9 = 120 ×T ※距離=速さ×時間
⇔T = 0.075(時間)
⇔T = 0.075×60(分)⇔ T = 4.5(分)
⇔T = 4分30秒
よって、先ほど「普通列車と出会ってから次の普通列車に出会うまで」の距離を求めていたので、この距離を走る際にかかる時間は4分30秒と求められました。
しかし、問題では「すれ違い終わってから次の列車と出会うまで」となっています。
下の図の赤い矢印の区間が9kmであり、この距離を走るのに4分30秒かかるとわかっています。
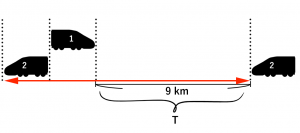
図より、すれ違う際の時間も求めてあげる必要があると分かります。すれ違う時間をxと置いてみましょう。
例として、時速120 km で走っている列車が、1台250 m の電車を追い越し終わるまでの時間を考えてみます。下記のように答えてしまう人がいるかもしれません。
250 m = 120km/h × x
これは誤答です。図を描いてみましょう。
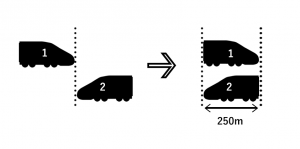
これでは、準急列車の先端が普通列車の後ろの端に到達したのにかかった時間になってしまいます。
列車同士がすれ違うということは、「列車の先端同士が並んだ状態から、列車の後ろ側の端同士が並んだ状態になる」と言い換えることができます。
よって図およびは次のようになります。
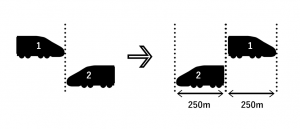
250 m + 250m = 120km/h × x
⇔500 m = 120km/h × x
⇔500/1000 km = 120km/h × x
⇔x = \(\frac{0.5}{120}\) (時間)
x = \(\frac{0.5}{120}\) ×60 (分)
x = \(\frac{0.5}{120}\) ×60×60 (秒)
x = 15(秒)
さて、実際の問題では「時速80km の上りの列車の準急列車が、下りの普通列車とすれ違い終わってから 次の普通列車と出会うまでの時間はいくらか?」であるので、先程の図を用いて考えてみたいと思います。

すると、求めたい時間は、(列車が出会ってから次の列車に出会うまでの時間)ー(列車同士がすれ違うまでの時間)を求めればいいとわかります。
よって、4分30秒―15秒 = 4分15秒
2番が正解だとわかります。


 個別指導講座
個別指導講座 お問い合わせ
お問い合わせ




