TOKUBETUの8文字を並べるとき、2つの T の間に他の文字が1つ以上入る並べ方は何通りあるか。特別区Ⅰ類（2019）

1：1260通り
2：2520通り
3：7560通り
4：8820通り
5：10080通り

順列の問題です。順列と聞くと難しく感じますが、いくつかのものを並び変えると並べ方は何パターンあるか？ということです。「並べ方は何パターンあるか？」を場合の数とも言ったりします。

異なるｎ個のものを並べるときは、n！で表せます。
ｎ！はn×(n-1) ×(n-2) ×(n-3) ×…×2×1と順番に掛け算するものでした。ｎから始まるので、これをｎの階乗と呼びます。

具体例で考えてみましょう。

例えば、SENDAIの6文字を並び替えるとその時の場合の数は、6×5×4×3×2×1=720通りできるとわかります。

では、KANAGAWAの8文字だとどうでしょう？同様に、8×7×6×5×4×3×2×1=40,320通りでしょうか？これでは不正解です。

SENDAIの例では全て違う文字でしたが、KANAGAWAでは同じAの文字が4つも入っています。

KANAGAWAでもKANAGAWAでも、黄色のAと青色のAを入れ替えて考えているにもかかわらず、色の区別を無くしてしまうと同じAという文字であるため、KANAGAWAとKANAGAWAのように区別がつかなくなってしまいます。

そしてこのように2文字同じ文字があると、全体の場合の数で同じ区別がつかない現象が起きるため、場合の数が本来の2！倍になってしまいます。

今回は4文字ダブりなので、場合の数は本来の４！倍多くなってしまいます。40,320通りとした誤解答は本来の場合の数よりも４！倍も多かったのですね。

ということは、ダブりがある場合は、（ダブりの文字数）！で割り算してあげればいいことになります。

KANAGAWAであれば8!÷4!=( 8×7×6×5×4×3×2×1)÷(4×3×2×1) = 1,680通りと求めることができました。

さらに具体例です。FUKUOKAの7文字だとUとKの2種類の文字のダブりがあるので、7!÷2!÷2! =で求められるとわかりますね。計算すると、(7×6×5×4×3×2×1)÷(2×1)÷(2×1) = 1,260通りです。

問題文を見ていきましょう。

この問題は二つの T の間に他の文字がひとつ以上入る並べ方を直接求めるのではなく、考えられる全通りから二つの T が隣接する並べ方を引き算する方法で求められます。

まず T の隣り合う条件を無視して8文字とも全て並べられる方法が何通りあるか考えます。

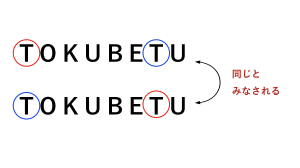
文字を見てみると T とUが同じ文字であることがわかります。これらは同じ文字であるため区別がついていないとみなされます。

よって1文字目のTと2文字目の T が入れ替わった場合と入れ替わらない場合とでは重複して数えてしまうことになります。よってこの重複した分を除いて数える方法を考えないといけません。Uも同様です。

その並べ方は下記の通りになります。

8!÷2!÷2! = (8×7×6×5×4×3×2×1)÷(2×1)÷(2×1) = 10,080通り…①

次に2つの T が隣接する並べ方を考えます。

これは2つの T をまとめて1つの文字とみなす方法です。つまりT２つを1文字として考えたので、全部で7文字(Uがダブり)の並べ方を考えます。

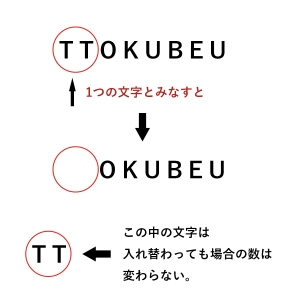
2つの T をまとめて1つの文字とみなした場合の計算方法は、以下の通りです。

7!÷2! = (7×6×5×4×3×2×1)÷(2×1) = 2,520通り…②

よって①②より、以上で求められたものを計算します。

10,080 – 2520 = 7,560通り

よって答えは3番とわかりました。