【問題】ある塾にA～Eの5人の中学生がいた。ある日この塾で国語と数学の試験が実施され、各試験の5人の平均点は国語が65点、数学が58点という結果であった。

いまア～オのことが分かっているとき正しいのはどれか。

ア：国語の平均点以上の生徒はA，Bの2人のみであり、1人は67点で、もう1人は86点であった。
イ：国語の最低点は51点であり、CとDの点数の差は3点であり、DとEのそれは8点であった。
ウ：数学の平均点以上の生徒は3人のみであり、Cが72点、Aが59点、残りの1人が63点であった。
エ：数学の最低点は41点であり、BとDの点数の差は14点であり、BとEのそれは8点であった。
オ：国語と数学の合計点の順位は、点数の高い方からA，C，B，E，Dの順であった。

1：Aの国語の点数は67点であった。
2：Bの国語と数学の合計点は122点であった。
3：Cの国語は点数の高い方から4番目であった。
4：Dの国語と数学の点数の差は10点であった。
5：Eの数学は点数の高い方から4番目であった。

（国家Ⅱ種2002）

与えられた情報を手掛かりに、Ａ～Ｅの点数がそれぞれ何点なのかを考えていきます。

アとイは国語の点数について書かれています。点数の高い順に並べると、

86点：AまたはB
67点：AまたはB
x点：CまたはDまたはE
y点：CまたはDまたはE
51点：CまたはDまたはE

ここで、平均点が65点であることが分かっているので、5人の点数の和は65×5＝325で、325点です。したがって、高い方から3番目と4番目の点数の和x＋yは、325－86－67－51＝121（点）

ところで、CとDの点差が３点でDとEの点差が8点という条件を満たす組み合わせは、以下の4通りしかありません。

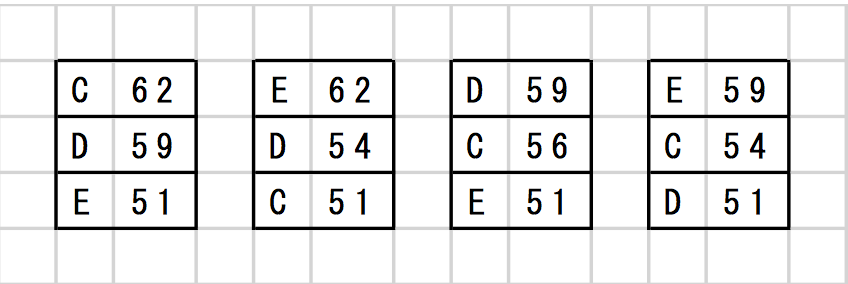
さらに、xとyの合計が121点という条件を満たすものは「C62点・D59点・E51点」の組み合わせしかあり得ないので、C・D・Eの点数が確定します。

なお、「平均点以上の生徒はAとBのみ」という条件も満たしています。

ウとエは数学の点数について書かれています。

平均点が58点であることが分かっているので、5人の点数の和は58×5＝290で、290点です。したがって、高い方から4番目の点数は、290－72－63ー59－41＝55（点）

点数の高い順に並べると、

72点：C
63点：BまたはDまたはE
59点：A
55点：BまたはDまたはE
41点：BまたはDまたはE

BとDの点差が14点でBとEの点差が8点となるのは、「E63点・B55点・D41点」の組み合わせしかあり得ないので、B・D・Eの点数が確定します。

なお、「平均点以上の生徒は3人のみ」という条件も満たしています。

ところで、AとBの国語の点数を確定することができませんでした。

ここで、国語と数学の合計点に注目します。オより、合計点ではAの方がBより高いということがわかります。

数学の点数がA59点・B55点ですから、国語の点数は「A86点・B67点」でなくてはなりません。

以上の情報より5人の点数を表にまとめると、以下のようになります。

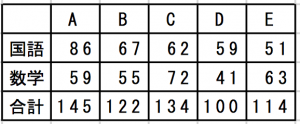
したがって、正解は選択肢2です。

―補足―

国語の点数のところでC・D・Eの点数と順位を確定しました。

気付いているかもしれませんが、実はこの問題はこれを確定しなくても解くことができます。

選択肢2はC・D・Eの点数や順位には関係ないからです。

本問のように、すべての情報をそろえる必要がない場合がありますので、注意深く選択肢を見ながら解くことも必要です。時間との勝負ですので、短縮できるところは短縮しましょう。