【問題】下図のように、点Pで、一部が着色された半径aの円Aが半径4aの円Bに内接し、円Bが半径2aの円Cに外接している。円Aは円Bの内側に接しながら、円Bは円Cの外側に接しながら、同じ速さでそれぞれ矢印の方向に滑ることなく同時に回転を始め、円Bがアの位置から円Cを半周してイの位置にきたとき、円Aの状態を描いた図として、正しいのはどれか。（東京都2008）

円の回転数の問題は頻出ではありませんが、基本的な解き方を押さえておけば難しくないので、解けるようにしておきたい分野です。

同時に考えるとややこしいので、

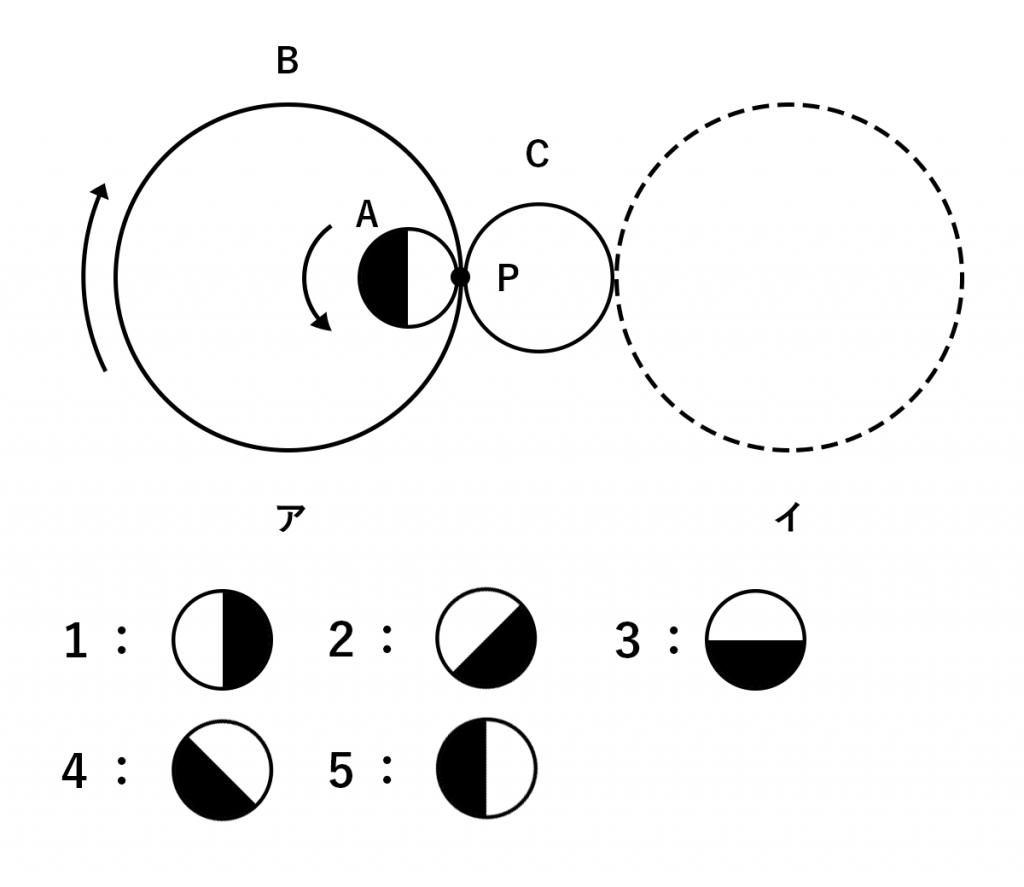
①円Cの外部を円Bが回転（円Ａは固定する）
②円Bの内部を円Aが回転（円Ｂは固定する）

このように2段階で考えます。

①円Cの半径：円Bの半径
＝2a：4a
＝1/2：1

したがって、円Bが円Cを半周したとき、円Bの回転数は
（1/2＋1）×1/2＝3/4

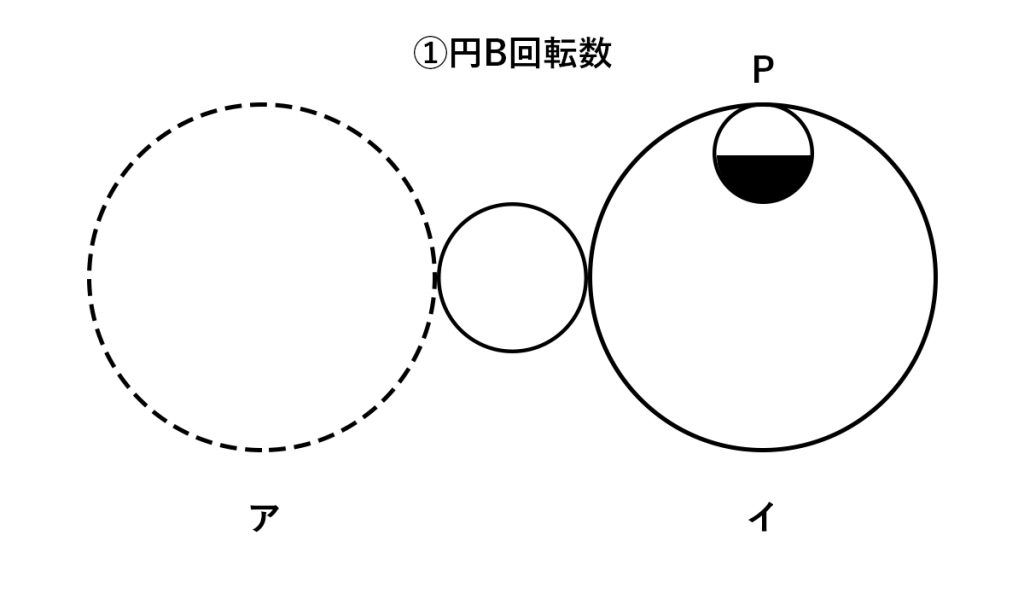
②円Aが円Bの内部を移動した距離は、①で円Bが円Cの外部を移動した距離、すなわち円Cの半周分に等しくなります。

円Bの半径は円Cの2倍なので、円Bの円周も円Cの2倍です。

したがって、円Aの移動距離は、円Bの1/4周分ということになります。

このとき、

円Bの半径：円Aの半径＝4：1

より、円Aの回転数は（4－1）×1/4＝3/4

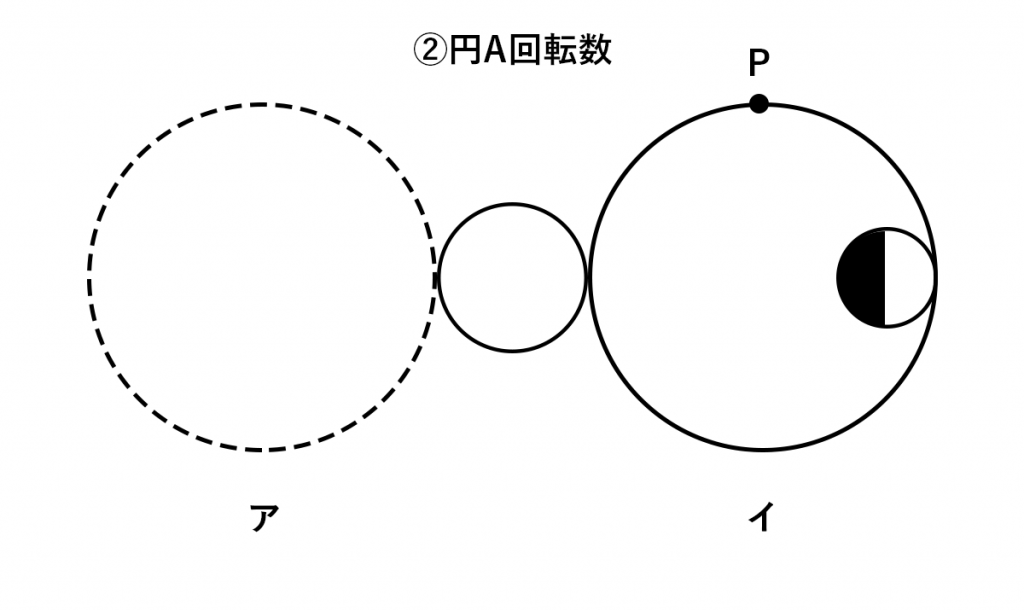
①と②が同時に起こるので、円Aは時計回りに3/4回転すると同時に半時計回りに3/4回転します。

すなわち、全く回転していないのと同じです。

したがって、正解は選択肢5です。

―補足―

円の回転数を求める考え方が、もうひとつあります。

固定された円に対して滑ることなく回転する円があるとき、その中心の移動距離を求めれば、それを円周の長さで割ったものが回転数になります。
これは外接していても内接していても成り立ちます。

今回の問題の場合、

①円Bの中心の移動距離は、半径3aの円の半周分、3aπとなります。

一方、円Bの半径は2aなので、円Bの円周は4aπです。

したがって円Bの回転数は、
3aπ/4aπ＝3/4

②途中まで、先程の結果を利用します。

円Aの中心の移動距離は、半径3aの円の1/4周分、すなわち3aπ/2となります。

一方円Aの半径はaなので、円Aの円周は2aπです。

したがって円Aの回転数は、
（3aπ/2）/2aπ＝3/4

このように求めることができます。