【問題】高校の同窓会で６人の同級生と同じテーブルになったが、顔と名前が一致しない。会話には姓とニックネームが入り混じっており、次のア～クのことが分かった。このとき、遠藤のニックネームはどれか。ただし、ニックネームは１人に１つとする。

ア：赤井と「あっちゃん」の２人は１年生のときＡクラスだった。
イ：岡田と「イツキ」の２人は１年生のときＢクラスだった。
ウ：宇野と「ウッチー」の２人は１年生のときＣクラスだった。
エ：井上と遠藤はサッカー部に所属し３年生のときにインターハイに出場したが、「ウッチー」 は２年生のときにサッカー部を退部している。
オ：「オメガ」はよく赤井に数学を教えてもらっていた。
カ：「カズさん」は宇野より英語の成績が良かった。
キ：井上と「あっちゃん」の２人は東京在住である。
ク：宇野と「オメガ」の２人は大阪在住である。

１：「あっちゃん」
２：「イツキ」
３：「エル」
４：「オメガ」
５：「カズさん」

（裁判所2009）

対応関係は全分野中最頻出で、「最も判断推理らしい分野」と言ってもよいと思います。情報の処理方法が他の分野にも通じるため、これを制すればいろいろな問題が解きやすくなります。

今回は、「名前」と「ニックネーム」の２項目が１対１に対応する、というシンプルな問題です。

基本的には下図のような対応表を書いて考えます。

対応項目が３要素になる場合にもこれを応用できるので押さえておきたいところです。

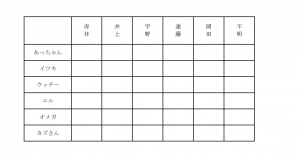
条件をひとつひとつ見ながら、あり得ない対応関係に×を記入していきます。

ア～ウより、クラスが違えば別人なので
赤井≠「あっちゃん」・「イツキ」・「ウッチー」
岡田≠「あっちゃん」・「イツキ」・「ウッチー」
宇野≠「あっちゃん」・「イツキ」・「ウッチー」
エより、井上≠「ウッチー」遠藤≠「ウッチー」
オより、赤井≠「オメガ」
カより、宇野≠「カズさん」
キ・クより、出身が違えば別人なので、
井上≠「あっちゃん」・「オメガ」宇野≠「あっちゃん」・「オメガ」

以上をすべて書き込むと、下図のようになります。

「エル」＝宇野、「ウッチー」＝苗字不明者（ここに名前が出てきていない）が確定しますので、「エル」と苗字不明者について、それ以外の対応関係はすべて×となります。

これを書き込むと、下図のようになります。

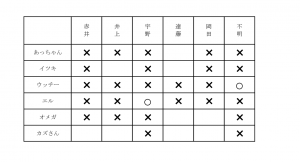
この時点で、「あっちゃん」＝遠藤と確定しますので、正解は選択肢１です。

対応関係の問題に限らず、「表などを最後まで完成させる前に正解にたどり着く」ケースは少なくありませんので、常に選択肢を注意深く見ながら解くことが大切です。

―補足―

表を最後まで完成してみましょう。

「カズさん」＝赤井と確定します。先ほどのように、遠藤と「カズさん」について、それ以外の対応関係はすべて×となります。

「オメガ」＝岡田が確定、それにより「イツキ」＝井上が確定します。

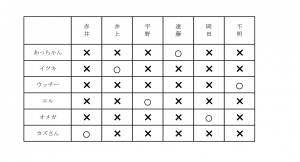
最終的には、下図のように対応表を矛盾なく埋めることができました。