A,Bの二人で交互に石を採り続け、最後の石を取った人が負けになるゲームをする。一度に採れる石は、一個3個4個のいずれかで、 AB の順にとるものとする。  AB はともに勝つために最善を尽くすとすると、石の数が4個から7個であればAが勝ち、石が8個であれば B が勝つ。石が10個の場合に関して正しく述べられているのはどれか。地上(1995)

１：Aは最初に一個取れば必ず勝つことができる。
２：A は最初に3個取れば必ず勝つことができる。
３：A は最初に4個取れば必ず勝つことができる。
４：最初のAが取る個数にかかわらず B は必ず勝つことができる。
５：A、B 共に必ず勝つ方法はない。

ゲームの必勝法に関する問題です。よく数字の何番を最初に取ったほうが勝つとかそういうゲームをしたことがあると思います。

今回の問題はそれによく似ていて、問題のゲームにも必ず勝てる必勝法というものがあるみたいです。問題のルールや条件をよく見て、必ず勝つ方法があるか考えてみましょう。

今回の問題文には、ある程度ヒントを与えてくれています。交互に石を取って行って、 A の番になった時に、 残った石の数が４，５，６，７個であれば、 Aの勝ちが確定し、 残った石の数が８個であれば、 B の勝ちが確定するようです。

読み替えると、自分の番に残りの石が４，５，６，７個であれば自分の勝ち、8個であれば相手の勝ちになってしまうようです。

またこのような問題の場合、自分が Bさんになったつもりになると、考えやすくなることが多いです。

「Aさんが取れる石は1個と3個と4個ある中、Aさんが〇個取ってきたら、Bさんが勝つためには△個取ろう」と考えることで、Aさんの取れる石の全パターンを条件ととらえ、Bさんの取れる石のパターンをその結果のようにして考えると、自然と問題文中の「A,Bはともに勝つために最善を尽くす」という条件を満たせます。

もちろん、Aさんが自分だと思って解くこともできるのですが、これは後攻の人になりきった方が、先行の人を条件とできるので考えやすいです。

選択肢一番の条件から考えていきましょう。

Aさんは最初に石を一個取りました。自分である Bさんが相手の Aさんを負けさせるには、相手の番になった時に残りの石を8個にしてやればいいことがわかります。残りの石は9個ですから、 Bさんは石を1個取れば必ず Aさんを負けさせることができます。 よって不適切であると考えられます。

選択肢の2番を見ていきましょう。選択肢１番と違って、相手の番に石が8個になるという条件を作れなくなってしまいました。しかしこれは逆に自分の定番に石が4個から7個であるという条件と合うことがわかります。

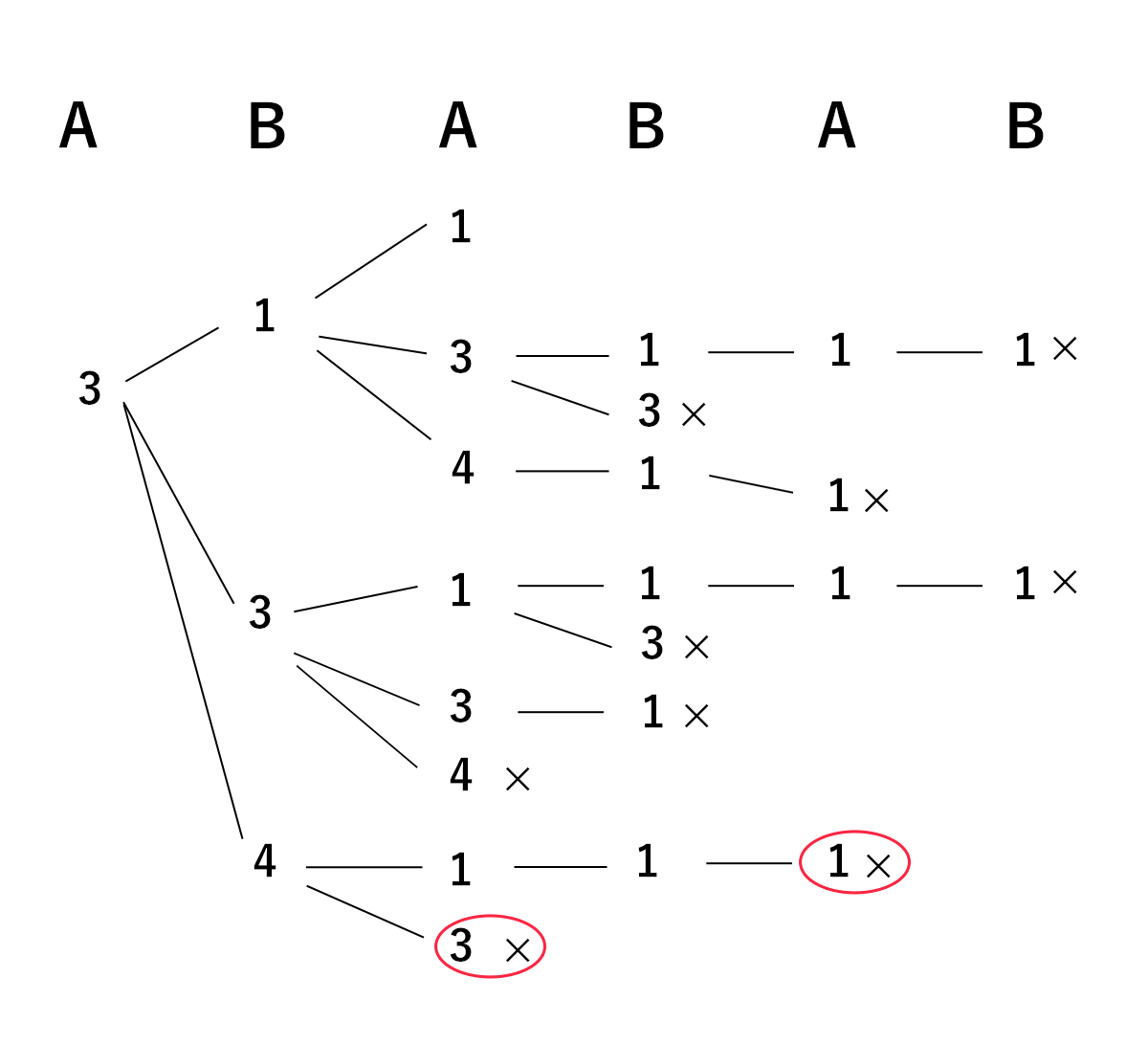
ここで、 Aさんの石の取りうるパターンとして樹形図を書いてみます。

樹形図を書くとなかなか大変で、膨大な作業に見えます。しかし一番数字が大きい箇所から書いていくと、場合分けの数も減るのでそこまで大変でもないです。

そして一番数字が大きい箇所を書き終えたところで、 Aさんが石を3個取った後 Bさんが4個石を取るという選択をすれば Bさんは必ず勝てることがわかります。よって選択肢2番は不適切であるとわかります。

選択肢3番を見ていきましょう。 こちらも同様にして樹形図を書いてみましょう。

こちらも同じく、大きい数字から樹形図を書いていくと、 Aさんが石を4個取った後、 Bさんは石を3個取れば必ず Aさんに勝てることがわかります。よって選択肢3番は不適切であるとわかります。

選択肢4番を見ていきましょう。これまでの選択肢1, 2, 3番を加味して考えると、どのパターンでも Bさんが勝つことができています。同時に選択肢5番は不適切であると分かります。

よって 正解は4番であることがわかります。