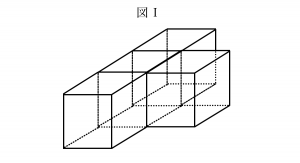
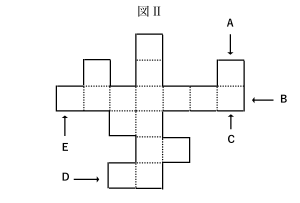
【問題】図Ⅰのように、同じ大きさの正方形を組み合わせて組み立てた立体があるこれを展開したところ、正方形の1枚を誤って切り落としてしまったため図Ⅱのようになった。切り落とした正方形を図ⅡのＡ～Ｅのどの部分に戻せば図Ⅰの立体の正しい展開図になるか。
ただし、図Ⅱの展開図の点線は、正方形どうしがつながっていることを表す。

１：Ａ
２：Ｂ
３：Ｃ
４：Ｄ
５：Ｅ

（国税・労基2007）

展開図では、組み立てたときに重なる辺のところに面を移動することができます。

例えば、下図は一般的な立方体の展開図ですが、赤い線のところは組み立てたときに重なります。このような場合、赤い線が重なるような位置に面を移動することができます。

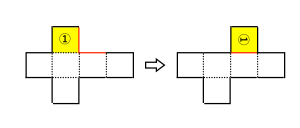展開図上で黄色の面①を移動しましたが、これを組み立てても同じ立方体になります。

更に、青い線の重なりに注目すると、下図のように黄色の面②③の移動が可能です。

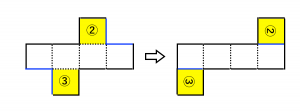
これを利用すると、一見複雑そうな展開図が見覚えのある展開図と同じであることに気づくことがあります。そうすることで非常に扱いやすくなります。

さて、図Ⅰの立体に、色を塗ってみました。すると、ピンク色の部分を芯として、そこに３色の積み木をくっつけたような形であることがわかります。

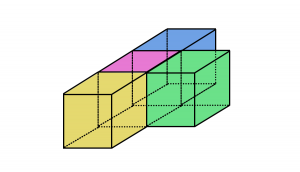
したがって、この立体の展開図は下図のようになります。

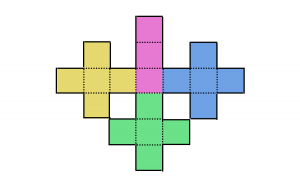
組み立てたときに重なる辺に注目しながら面の移動をすると、図Ⅱとよく似た展開図になります。

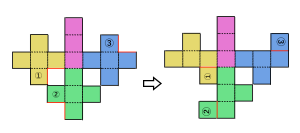
ところが、下図の赤く塗った部分だけが足りません。

このことより、誤って切り落としてしまった箇所はこの部分だったということがわかります。

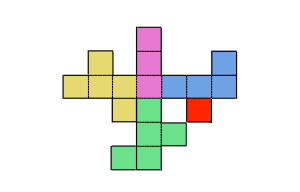
同じ立体を作るためには、この赤く塗った部分を展開図上で移動可能な場所に戻さなくてはなりません。

選択肢中で移動可能なのは、Ｃの場所しかあり得ないので、正解は選択肢３です。